DTU Compute, Matematik 1, MatTek1-holdet, 2014-2015


Temaøvelser

Temaøvelserne nr. 1-3 afvikles i efteråret 2014, og nr. 4-5 i foråret 2015. Temaøvelserne er et selvstændigt kursus 01008 på DTU.

Testene efter hver temaøvelse er multiple choice. Læs om bedømmelsen.

Temaøvelser

Om temaøvelserne: om-tema.pdf

Grupper til temaøvelser: grupper.pdf

Maple Cloud til udveksling af filer
God ide til gruppearbejdet!

 Temaøvelse 1 (Markov-processer)

  • Markov proces
  • Markov Processes
  • Markov process
  • Markov chain
  • Markov chain (Google billeder)
  • Stochastic process
  • Markov biografi

    Induktions-bevis:
  • Mathematical induction
  • Induktion (matematik)
  • Matematisk induktion (Georg Mohr)

    Maple-kommando:
  • seq (kan generere en følge af matrixpotenser Ak)

  • Blok-maticer, enhedsmatricer & nulmatricer:
        blok-mx.mw eller blok-mx.pdf

    		• Temaøvelse 2 (Skalainvarians af flodsystemer)

  • Hack's_law
  • Scale_invariance

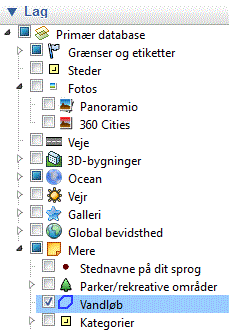
    Vedr. Google Earth: "Water body outlines" hedder på dansk
    "Vandløb" (ligger under "Mere" i "Lag")!


    "PowerFit" fra Statistic-pakken kan anvendes.
    "PowReg" fra Gym-pakken kan anvendes.
    "LinReg" fra Gym-pakken kan anvendes efter en transformation af
    dataene: brug ln~ på listerne. Læs om brugen af ~ i Maple

    • Temaøvelse 3 (Nedbrydning af pesticider)

    Kilde:
    Baggrundsartiklen kan hentes via DTU bibliotek:
    findit.dtu.dk/en/catalog/6279575
    "Determination of soil biodegradation half-lives from simulation
    testing under aerobic laboratory conditions - A kinetic model approach".

    Compartment model:
    Opstilling af differentialligningssystemet er en generel metode, kendt
    under navnet "compartment model", som er en god illustration til
    at opstille differentialligningerne ud fra ændringer af stofmængderne.
    Ændringerne findes simpelthen som +input og -output!
    Man tegner kasser (stofmængder) og pile (input/output).
    Internet-inspirationskilder:
    Google billedsøgning på "compartment model"
    Compartmental models in epidemiology
    Pharmacokinetics
    Compartment models (Blomhøj Kjeldsen Ottesen, 47 sider, 2014)

    Successiv løsning:
    Differentialligningssystemet er sådan opbygget, at det kan løses én
    differentialligning ad gangen! Koblingen er således ikke alvorlig.
    Her er successiv løsning et alternativ til teorien om systemmatricer og
    egenværdier til løsning af systemet.
    Metode:
    1. ligning løses mht. P(t).
    P(t)-løsningen indsættes i ligning 2, som så kan løses mht. M(t).
    Løsningerne for P(t) og M(t) indsættes i ligning 3, som løses mht. N(t).
    Løsningen for M(t) indsættes i ligning 4, som løses mht. V(t).
    Pga. systemets natur vil alle løsningerne bestå af eksponentialfunktioner,
    og de mange konstanter kPM, kPN, kMN, kMV vil indgå.

    Numerisk løsning:
    Overskriften i opgave 2 er "numerisk løsning". Det er misvisende!
    Numerisk løsning af et differentialligningssystem vil sige, at man løser
    det tilnærmet med numeriske metoder, f.eks. Runge-Kutta.
    Runge–Kutta methods
    Det er nødvendigt, når systemet ikke kan løses analytisk, dvs. eksakt.
    Eksempel på differentialligningssystem, som skal løses numerisk, er
    SIR-modellen for udbredelse af epidemi. Løsningen med dsolve tilføjes
    parametren "numeric", og plotning sker med "odeplot":
    sirmodel.mw eller sirmodel.pdf

    Middelværdi og amplitude:
    Hvordan beregner man den asymptotiske middelværdi og amplitude af
    en svingning? limit.mw eller limit.pdf
    Formel for amplituden af a·cos(x)+b·sin(x):
    amplitud.mw eller amplitud.pdf

    		Temaøvelse 4 (Snowball Earth)

    Kilde:
    Baggrundsartiklen kan hentes via DTU bibliotek:
    findit.dtu.dk/en/catalog/56948740
    "Snowball Earth", Scientific American, år 2000, vol 282, side 68-75.

    Idealized_greenhouse_model

    "The global energy balance": www.geo.utexas.edu/
    courses/387H/Lectures/chap2.pdf
    		Temaøvelse 5 (Skovbrand)

  • DTU Byg: Master i Brandsikkerhed

  • Artiklen "Brand!" fra bogen Matematiske Horisonter
    eBogen fylder 11.4 MB, artiklen står side 51-62.
    Artiklen er skrevet af professor Steen Markvorsen, DTU Compute.

    Artikel af G. D. Richards: "An Elliptical Growth Model of Forest Fire
    Fronts and its Numerical Solution    ", International Journal for Numerical
    Methods in Engineering, Vol. 30, 1163–1179 (1990):
    findit.dtu.dk/en/catalog/164954377

    Artikel af Jan Glasa & Ladislav Halada: "On elliptical model for forest
    fire spread modeling and simulation    ", Mathematics and Computers in
    Simulation 78 (2008), s.76–88:
    findit.dtu.dk/en/catalog/6717409

  • Wildfire
  • Wildfire Modeling
  • List of Wildfire
    		•